這是一個我從很久以前就有的想法,印象中最原始的想法大約始於國中期間,當時甚至都還沒在學校學到極限的觀念。一直到高中、大學之後我才漸漸對相關數學有足夠的理解,然而問題還是沒有解決。
記得當年和小豪討論過這個問題,不過忘掉最後是否得出有意義的答案。
雖然後來我看過這個問題比較簡單的變形,不過我還是以最初的想法來描述
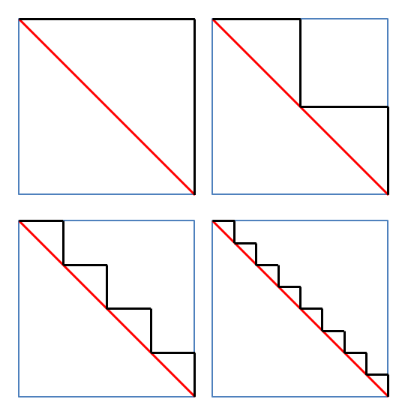
假設有一個正方形邊長為1,那麼對角線如紅色所示,長度為根號2;圖中沿正方形兩邊的黑線長度為2。
將黑線改成階梯狀,長度依然是2。不難看出反覆分解下去,階梯會越來越小且階數越來越多,但總長度並不會因此改變。
有趣的地方來了,當分解數趨近無限的時候,最後黑線會無限趨近紅線,那時候黑線的長度應該是多少?
如果黑線等於紅線,那麼長度應該為根號2
但若是按照剛才前幾回合的例子來看,應該是不管再怎麼分割長度還是維持2不變。
*********
雖然看起來很為反直覺,其實有限操作和無限操作所得到的長度確實是不同的。
這個例子很清楚的示範,有限逼近的性質不見得會在無限逼近中保留,所以在探討問題時慎選欲逼近的性質很重要。
*********
2010/11/05 補充
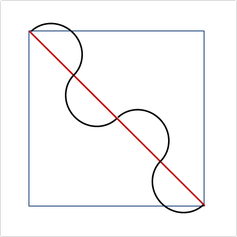
這個問題還有其他變形,最常見的似乎是正三角形和本文示範的直角三角形,另外用半圓形也是一種做法
全站熱搜


 留言列表
留言列表