close
在前一篇中我介紹了托里切利的 Vuvuzela,不過其中有個無限延伸的 x 軸讓人難以接受,並且要用到稍微麻煩的微積分計算。
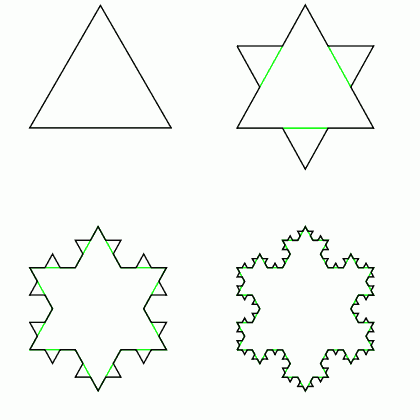
在這篇我想補充一個有點類似的問題,改自於數學家 Helge von Koch 提出的 Koch 雪花曲線。一開始我們有一個正三角形,然後我們把各邊中央取三分之一再長出小三角形,成為六角星形。這個步驟可以繼續持續下去,直到無限。
稍微觀察即可發現,第 n 步的時候周長會變為初始三角形的 (4/3)^n 倍,也就是說當 n 趨近無窮的時候週長也會發散到無窮大。
然而當 n 趨近無窮大 時面積成長卻是收斂的,最後會收斂到初始三角形的 8/5 倍。
接下來我們拿這個圖形當作底面,做出一個深度為 d 的游泳池。當然在現實中會遇到一些問題,因為照 Koch 的定義,這些轉折很快就會降到微米、奈米等級,然後迅速降到比原子還要小。
不過在數學世界我們可以把這個問題拋諸腦後,最後會得到一個體積有限但表面積無窮大的游泳池。然後我們比照前例,要求將游泳池內壁漆成水藍色,但是由於泳池內壁面積無窮大,所以窮盡全世界的漆都辦不到。可是又因游泳池體積是有限的,所以要將整個泳池裝滿漆並不難。
關於這個問題的解釋法可以參考小豪在前一篇的意見
全站熱搜


 留言列表
留言列表