元旦看到一個有趣的物理問題,現在才有空寫一些想法。有一位細心的網友(大概也沒人沒他跨年吧)發現教科書上寫道:「角位移不能視為向量」,於是感到很好奇。不過更讓他好奇的是,角速度竟然可以視為向量,而角速度僅僅是角位移除以時間單位而已。
因為有些網友可能不清楚角位移、角速度這些名詞,或者是曾經學會但是現在忘了,所以這裡複習一下。
角位移(angular displacement)其實很容易理解,它是用來描述轉動程度的量,通常用弧度、角度、圈數作單位。舉例來說,當手表的秒針從 12 點轉到 6 點,那麼我們可以說秒針的角位移是順時針轉半圈,不過在科學上比較喜歡用順時針轉 pi 弧度這種描述方式。同樣的,如果秒針逆向整整轉了一圈,那麼角位移就是反時針轉了 2pi 弧度。
角速度(angular velocity)則是每單位時間內的旋轉量,和口語上的轉速概念是一樣的,只是物理上比較喜歡用弧度來描述。舉例來說,秒針每60秒轉 2pi 弧度,所以平均角速度就是順時針 2pi/60 (rad/sec)。不過因為秒針並非均勻的旋轉,而是跳格式的運動,所以秒針的瞬時角速度很難描述。
對轉動有點概念的人應該可以理解,像是「順時針轉pi弧度」這樣的量是可以用一組「大小」和「方向」來描述的。例如我們慣用右手座標系的人可能會這樣,以弧度作為量的大小,而順、反時針則可以用右手規則定出一個方向。雖然可以用「大小」和「方向」來描述角位移,可是角位移卻不是向量。
我記得以前念書的時候,老師不停強調向量就是有大小、有方向。但隨著書讀多了漸漸明白並不是如此,這是一個過度簡化、甚至錯誤的說法。(還有另一個常見的誤用就是把所有n-tuple都看成向量,這也不一定成立。)
一個東西若能當成向量,不僅僅是有大小、方向而已,更重要的是必須滿足向量操作的條件。角位移之所以不是向量,就是因為他不能滿足向量加法交換律和結合律。其實這個道理很簡單,只是告訴我們多個旋轉以不同順序「加」在一起會有不同的效果,參看下圖。
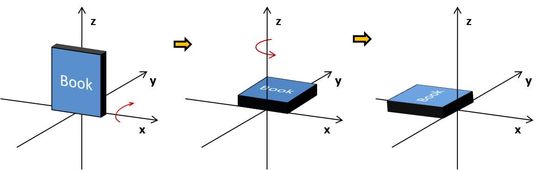
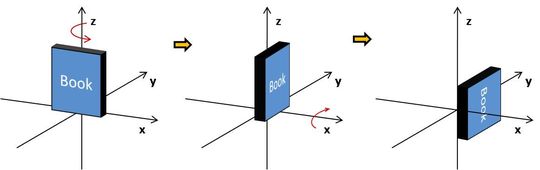
例外的情況是無限小的旋轉,也就是轉動量無限趨近於0,此時向量加法交換律和結合律就可以滿足,這就是為何瞬時角速度可以當成向量來看待。如果我們將旋轉的維度限制在同一平面上,向量加法交換律和結合律也是可以被滿足的。(不過這裡要提醒的是,用右手規則製造出來的向量仍然和真正的向量有一點點不同)
或許有人會疑惑,是不是向量有那麼重要嗎?不就只是個名稱分類而已。誠然,這些就只是數學家沒事訂出來的名詞與分類,但數學家沒事之餘也對這些東西的性質做了非常大量的探討,當有人說「某某可以視為向量」時不僅僅是在數學上做分類,而是在說數學家在向量方面累積的全部知識對這件事情都管用。不論是物理學的力與場,或是機器學習當中由參數構成的高維抽象空間,只要能夠用向量、梯度來表示,那麼我們就可以用相同的數學來進行操作。
所以「角位移不能視為向量」這個陳述的意義在於,很多對向量管用的操作碰到角位移不一定成立,例如欲將多個獨立的角位移加起來合成一個新的操作,就必須注意順序問題,否則結果可能會和預期大大不同。


 留言列表
留言列表