novus log

著名的物理學家托里切利(Evangelista Torricelli)曾師事加利略，他除了製造托里切利真空之外，另一項比較不有名的成就是以數學方式描述 Vuvuzela。

方式是這樣的：

取函數 y = 1/x，其中 x 域定義為 x >= 1，作出此函數圖形，然後將圖形沿 x 軸轉一圈成為錐狀立體。

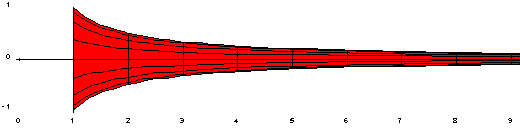
這個圖形有些人稱為托里切利小號(Torricelli's Trumpet)，也有人稱為加百列的號角(Gabriel's Horn)，不過我很不喜歡這個名稱，因為會搜尋到一堆惱人的宗教文。比較傳神的名稱應該是托里切利的 Vuvuzela 吧。

看起來好像沒有太特別的地方，不過托里切利發現一件很有趣的事，那就是這個這個形狀的體積是有限的，可是表面積卻無窮大。

用微積分可以算出這個形狀的體積

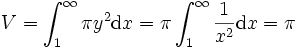
同樣可以算出表面積

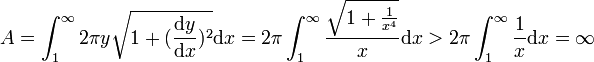
其實托里切利過世的那一年，牛頓才4歲、萊布尼茲才1歲，所以托里切利還沒有微積分可以用，不過這不是重點。

如果你還沒發現這有什麼不對，請想像一下如果有人請你把這支 Vuvuzela 漆成黃色是什麼情形？由於表面積無窮大，所以用盡全地球的漆也辦不到。

但其實還有一個簡單的做法，我們可以把這支無限長的 Vuvuzela 立起來，由於體積是有限的，所以我們很容易就可以倒入 pi 單位的漆將其填滿，等到漆附著在表面上後把多餘的漆倒掉即可。